Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation | |
|
The Turing, or reaction-diffusion (RD), model is one of the best-known theoretical models used to explain self-regulated pattern formation in the developing animal embryo. Although its real-world relevance was long debated, a number of compelling examples have gradually alleviated much of the skepticism surrounding the model. The RD model can generate a wide variety of spatial patterns, and mathematical studies have revealed the kinds of interactions required for each, giving this model the potential for application as an experimental working hypothesis in a wide variety of morphological phenomena. In this review, we describe the essence of this theory for experimental biologists unfamiliar with the model, using examples from experimental studies in which the RD model is effectively incorporated.
См. сайт Лаб. |
В последние 30 лет исследования на молекулярном уровне выявили широкий круг физиологических феноменов, регулируемых с помощью сложных сетей клеточных и молекулярных взаимодействий (1). Сложность таких сетей ставит новые проблемы, однако, т.к. поведение таких систем часто не поддаётся непосредственному или интуитивному пониманию. Математические подходы могут помочь облегчить понимание сложных систем и, кстати, эти подходы приняли две первичные формы. Первая использует анализ каждого элемента сети количественно и моделирует все взаимодействия на компьютере (1). Эта стратегия эффективна на относительно простых системах, таких как метаболический путь в одиночной клетке и активно используется в области системной биологии. Однако в более сложных системах, в которых пространственно-временные параметры имеют значение, становится почти невозможно сделать осмысленные предсказания. Вторая стратегия, одна из которых включает простое математическое моделирование, в котором детали системы опущены, может быть более эффективной в экстрагировании природы сложных систем(2). Реакционно-диффузионная (RD) модель (3) предложена Alan Turing является шедевром такого типа математического моделирования, которое может объяснить, как автономно формируются пространственные паттерны.
В RD модели Turing использует простую систему "two diffusible substances interacting with each other" , чтобы представить механизмы формирования паттерна у эмбрионов и установил, что такие системы могут генерировать автономно пространственные паттерны. Наиболее революционным свойством RD модели явилось введение "reaction", которая продуцирует лиганды (морфогены). Если "diffusion" действует одна, то локальные источники морфогенов необходимы, чтобы сформировать градиент. В таком случае позиционная информация, задаваемая системой зависит от препаттерна (Fig. 1, A and B). При введении реакции система пополняется способностью генерировать различные паттерны независимо от препаттерна (Fig. 1C). К сожалению, Turing умер вскоре после опубликования своей плодотворной работы, но модельные исследования модели показали, что эта система может воспроизводить большинство биологических пространственных паттернов (4-6). Позднее был предложен ряд математических моделей (4) , но большинство следовало базовой идее Turing's, что "the mutual interaction of elements results in spontaneous pattern formation." Модель RD сегодня признается как стандарт среди математических теорий, которые имеют дело с формированием биологических паттернов.
Однако эта модель всё ещё не получает широкое признание среди биологов экспериментаторов. Одна из причин брешь между математической простотой модели и сложностью реального мира. Гипотетические молекулы оригинальной RD модели идеализированы по причинам математического анализа, так что кажется почти невозможным адаптировать модель непосредственно к сложным реальным биологическим системам. Однако это недоразумение, которому поддаются экспериментальные исследователи. Логика формирования паттерна может быть понята с помощью простой модели и путем адаптации этой логики к сложным биологическим феноменам, она становится для извлечения из неё сути лежащих в основе механизмов. Геномные данные и новые аналитические технологии сдвинули цель исследователей развития с идентификации молекул к пониманию поведения сложных сетей, сделав RD модель даже более важным инструмента для теоретического анализа.
 Fig. 1. Schematic drawing showing the difference between the morphogen gradient model and Turing model. (A) A morphogen molecule produced at one end of an embryo forms a gradient by diffusion. Cells "know" their position from the concentration of the molecule. The gradient is totally dependent on the prepattern of the morphogen source (boundary condition). (B) Adding a second morphogen produces a relatively complex pattern; but with no interactions between the morphogens, the system is not selfregulating. (C) With addition of the interactions between the morphogens, the system becomes selfregulating and can form a variety of patterns independent of the prepattern. [Art work by S. Miyazawa]
Fig. 1. Schematic drawing showing the difference between the morphogen gradient model and Turing model. (A) A morphogen molecule produced at one end of an embryo forms a gradient by diffusion. Cells "know" their position from the concentration of the molecule. The gradient is totally dependent on the prepattern of the morphogen source (boundary condition). (B) Adding a second morphogen produces a relatively complex pattern; but with no interactions between the morphogens, the system is not selfregulating. (C) With addition of the interactions between the morphogens, the system becomes selfregulating and can form a variety of patterns independent of the prepattern. [Art work by S. Miyazawa] The Original Turing Model
В начале своей оригинальной работы (3), Turing отмечает, что его цель показать, что комбинация известных физических элементов достаточна, чтобы объяснить формирование биологических паттернов. Элементы, отобранные Turing , это теоретическая пара взаимодействующих молекул, распространяющихся в непрерывном поле. В своём математическом анализе Turing установил, что такая система даёт 6 потенциально устойчивых состояний, в зависимости от динамики вреени реакции и длины волны паттерна [Fig. 2A and Supporting Online Material (SOM) Text 1-1]. В случае I, система сводится к стабильному и униформному состоянию. В случае II, возникает униформная фаза осцилляций концентраций морфогена. Такая фаза унификации наблюдается в таких системах как циркадные ритмы (7) с сокращение мышечных клеток сердца (8). В случае III, система формирует паттерны типа соль-и-перец, такие как возникающие. когда дифференцированные клетки ингибируют дифференцировку соседних клеток. Это наблюдается. напр., когда дифференцируются клетки нервных предшественников в эпителии эмбрионов дрозофилы (9). Случай IV представляет собой необычное состояние, при котором паттерн сортировки, полученный в случае III, осциллирует. Примеры подобного не обнаружены в развивающихся системах. В случае V, генерируется распространяющаяся волна. Биологические путешествующие волны, вызываемые этим механизмом, включают спиральные паттерны, формируемые социальными амёбами Dictyostelium discoideum при агрегации (10), и волны ионов кальция, которые пересекают яйцо лягушки Xenopus laevis в ответ на проникновение спермия (11).
В случае VI, возникают стационарные паттерны. Находка этого типа волн является крупным достижением Turing's анализа, они обычно обозначаются как Turing patterns. Тьюрингов паттерн это тип нелинейной волны, которая поддерживается за счёт динамического равновесия системы. Длина его волны детерминируется с помощью взаимодействий между молекулами и скоростями их диффузии. Такие паттерны возникают автономно, независимо от какой-либо предсуществующей позиционной информации. [Дополнительные материалы содержат расширенное объяснение RD модели для биологов, которые мало знакомы с математическим описанием (SOM Text S1-1), а также дается математическое объяснение того, как возникает периодический паттерн в системе (SOM Text S1-2).] Это свойство позволяет объяснить, как паттерны возникают точно в, напр., оплодотворенных ооцитах, в которых присутствует мало позиционной информации. Способность Тьюринговых паттернов регенерировать автономно, даже после экспериментально вызванных нарушений, также важна и несёт большую пользу для объяснения автономности, выявляемой в паттерн-формирующих процессах развития (4, 6). Кроме того, благодаря тонкой настройке параметров и пограничных условий, система, лежащая в основе формирования Тьюрингова паттерна, может генерировать почти безгранично разнообразие пространственных паттернов. (Рис. 2B представляет образцовые двумерные паттерны, полученные при моделировании с помощью RD модели.) Замысловатая спиральная закрученность ракушек (5), совершенный паттерн перьев (12) и захватывающее дух огромное разнообразие паттернов кожи позвоночных (13) всё это было смоделировано внутри каркаса Turing модели (Fig. 2C). Удивительное сходство между предсказанием и реальностью в этих моделированиях строго подчеркивает, что Тьюринговы механизмы являются лежащими в основе принципами в этих и др. способах формирования биологических паттернов. (User-friendly simulation software is available as supporting online material; a manual of the software is in SOM Text 1-3.). Compatibility of RD and Gradient Models
Экспериментальные биологи могут сказать, что "gradient model" довольно эффективна в объяснении паттерн-формирующих событий (14). В классической градиентной модели фиксированный источник морфогена в специфическом положении предоставляет позиционную информацию (14) (Fig. 1). Хотя предположение о источнике морфогена, по-видимому, отлично от предположений RD модели, оно может быть внесено в RD модель довольно естественно, в качестве "boundary condition." Др. словами, классическая модель градиента морфогена, может рассматриваться как специфический случай RD модели, при котором reaction term устранен. Во многих исследованиях по моделированию такие пограничные условия используется, чтобы сделать паттерн более реалистичным (6). Недавние экспериментальные исследования градиентов морфогенов показали, что точность и ошибкоустойчивость градиента обеспечивается с помощью взаимодействий молекулярных элементов (15). Чтобы смоделировать такие ситуации авт. использовали математическую структуру, которая в основном идентична таковой RD модели. Как реакция, так и пограничные условия являются существенными для понимания сложности реальной системы и модель RD пригодна для моделирования таких случаев. Applying the "Simple" RD Model to a Complex Reality
Гипотетические молекулы в оригинальной RD модели (3) были идеализированы для удобства математического анализа. Предполагалось, что они контролируют свой собственный синтез и синтез их противников (counterparts) и быстро диффундируют по пространствам, которые д. быть подразделены клеточными мембранами. Очевидно, что довольно трудно приложить такую модель непосредственно к сложным живым системам.
Совместные усилия по наложению теоретических моделей на системы реального мира, однако, приносить плоды, подчеркивая, что более широк круг ситуаций, в которых генеральные принципы, лежащие в основе модели Тьюринга могут быть применены. Gierer and Meinhardt (16, 17) показали, что система нуждается лишь во включении сети, которая комбинирует "a short-range positive feedback with a long-range negative feedback", чтобы генерировать Turing паттерн. Это сегодня принимается как базовая потребность для формирования паттерна Turing (14, 16). Это усовершенствование сделало типы и количества реагирующих факторов неспецифицированными, делая это более простым, чтобы представить себе системы, которые могут удовлетворять потребностям.
Необходимые взаимодействующие элементы не д. быть ограничены молекулами или даже дискретными сущностями (entities); circuit клеточных сигналов также д. действовать (18). Имеется также необходимость в стимулах, предоставляемых посредством диффузии; др. способы трансмиссии могут быть достигнуты с тем же самым результатом. Теоретическое моделирование показало, что переключаемые серии непосредственных межклеточных сигналов могут формировать волну, обладающей свойствами, сходными с таковыми, формируемыми диффундибельными факторами (19). Др. формы передачи сигналов, включая хемотактическую миграции клеток (20), механохимическую активность (21), и взаимодействия нейронов [как в модели Swindale (22) ocular доминирования в формировании полосок], также способны формировать Turing-подобные паттерны. Во всех этих системах, формируются сходные периодические паттерны, где выполняется условие "short-range positive feedback with long-range negative feedback".
Почему системы, описываемые безусловно разными уравнениями ведут себя одинаково и какова ёмкость паттерн-формирующих различий между ними, это важные вопросы в математической перспективе. Но если динамика систем является почти той же самой, то экспериментальные исследователи могут выбирать любую модель в качестве своей рабочей гипотезы. В случает формирования паттерна кожи рыб, хотя эксперименты с очевидность показывают участие механизма трансдукции недиффундирующего сигнала, простейшая RD модель может предсказать перемещение паттерна во время роста рыб (23) и необычные паттерны, наблюдаемые у гибридных рыб (24). Finding Turing Patterns in Real Systems Во время эмбриогенеза возникает большое разнообразие периодических структур из различных не периодических клеточных или тканевых источников, указывая тем самым, что волны типа генерируемых по Тьюрингу или родственные механизмы могут лежать в основе широкого круга онтогенетических процессов. Используя современные генетические и молекулярные техники возможно идентифицировать предполагаемые элементы сетей диалоговой связи (interactive networks), которые удовлетворяют критериям коротко-действующией позитивной обратной связи и дально-действующей негативной обратной связи, но находка только сети недостаточна. Скептики справедливо указывают, что просто потому, что если имеется вода, не следует иметь в виду волны. Не имеет значения, насколько ярко или верно математическое моделирование может воспроизводить действительный биологический паттерн, только это не является доказательством, что моделируемые состояния отражают реальность. Это является др. крупным препятствием в идентификации неотразимых примеров Turing паттернов в живых системах. Решение, однако не столь запутанно; чтобы показать, что волны существуют, нам надо идентифицировать динамические свойства паттерна, которые предсказываются компьютерным моделированием. Экспериментальные демонстрации сконцентрированы на формировании паттерна в коже, поскольку специфические характеристики Turing паттернов наиболее доказательны в двух измерениях скорее, чем в одном. Turing Patterns in Vertebrate Skin Наблюдение динамических свойств Turing паттернов в природе сделаны Kondo and Asai
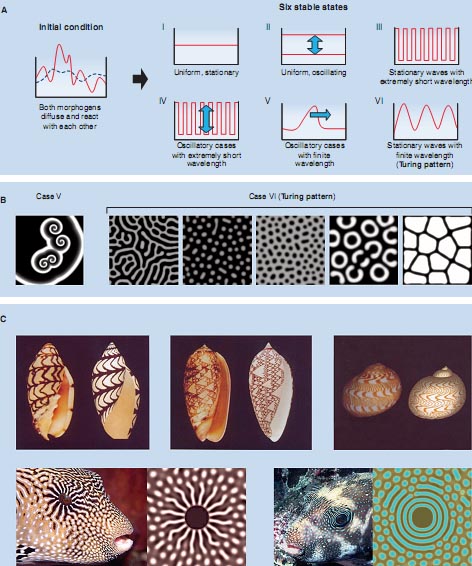 Fig. 2. Schematic drawing showing the mathematical analysis of the RD system and the patterns generated by the simulation. (A)Sixstablestates toward which the two-factor RD system can converge. (B)Two-dimensional patterns generated by the Turing model. These patterns were made by an identical equation with slightly different parameter values. These simulations were calculated by the software provided as supporting online material. (C) Reproduction of biological patterns created by modified RD mechanisms. With modification, the RD mechanism can generate more complex patterns such as those seen in the real organism. Simulation images are courtesy of H. Meinhardt [sea shell pattern (5)] and A. R. Sandersen [fish pattern (13)]. Photos of actual seashells are from Bishougai-HP (http://shell.kwansei.ac.jp/~shell/). Images of popper fish are courtesy of Massimo Boyer (www.edge-of-reef.com).
Fig. 2. Schematic drawing showing the mathematical analysis of the RD system and the patterns generated by the simulation. (A)Sixstablestates toward which the two-factor RD system can converge. (B)Two-dimensional patterns generated by the Turing model. These patterns were made by an identical equation with slightly different parameter values. These simulations were calculated by the software provided as supporting online material. (C) Reproduction of biological patterns created by modified RD mechanisms. With modification, the RD mechanism can generate more complex patterns such as those seen in the real organism. Simulation images are courtesy of H. Meinhardt [sea shell pattern (5)] and A. R. Sandersen [fish pattern (13)]. Photos of actual seashells are from Bishougai-HP (http://shell.kwansei.ac.jp/~shell/). Images of popper fish are courtesy of Massimo Boyer (www.edge-of-reef.com).при изучении горизонтальных полосок у тропических рыб, Pomacanthus imperator (25). Они недавно показали, что подобной динамической природой обладают многие виды рыб , включая хорошо известные организмы, рыбки данио. Хотя плоски рыбок данио могут казаться стационарными, экспериментальные пертурбации паттерна запускаются замедленными изменениями (23). Вследствие устранения лазером пигментных клеток в паре чёрных горизонтальных полосок нижняя линия сдвигается вверх перед стабилизацией в колокол-подобную кривую (Fig. 3A) (23). Как результат, пространственный интервал между линиями сохраняется, даже если их направление меняется. Это поразительное поведение предсказывается моделированием (Fig. 3B). К счастью рыбки данио пригодны для различных экспериментальных подходов, которые могут приводить к идентификации circuit взаимодействий, которые генерируют эти паттерны (26). Исследования показали, что паттерны кожи этих рыб закладываются и поддерживаются путем взаимодействий между пигментными клетками (26). Nakamasu разработал сеть взаимодействий среди пигментных клеток. Хотя форма сети отличается от той, что в оригинальной модели Тьюринга, она согласуется с описанием коротко-действующих позитивных и дально-действующих негативных обратных связей (18). (Взаимное ингибирование между чёрными и желтыми клетками ведет себя как позитивная петля обратной связи, т.к. экспансия чёрных клеток ослабляет их противников). Идентификация генетических факторов, участвующих в пигментации рыбок данио проводится (26), и есть надежда, что это сможет объяснить детали сигнальной сети, лежащей в основе волн в коже рыб и потенциально у всех позвоночных. Множество сходных поверхностных паттернов, обнаруживается у беспозвоночных и растений. Мы предполагаем, что в этих случаях лежит по сути сходный механизм (RD mechanism), хотя его молекулярные основы могут быть другими.
Др. хорошо изученными примерами являются регулярные закладки зачатков перьев у цыплят (27), и волосяных фолликулов у мышей (28). Jung et al. показали, что пространственно периодические паттерны зачатков перьев регенерируют даже когда кожа рекомбинирована из диссоциированных клеток (27). В случае волосяных фолликулов мышей альтерации количеств предполагаемых ключевых факторов меняют паттерн по типу, предсказанному компьютерным моделированием. Sick et al. использовали избыточную экспрессию и ингибирование Wnt и Dkk у плодов мышей, чтобы исследовать как пертурбации могут влиять на формирование паттерна фолликулов (28). С помощью моделирования они сначала предсказали, что кольцевой паттерн экспрессии гена Wnt, который не наблюдается в природе, может давать эктопическую продукцию белка Wn, где он контролируется соотв. и затем подтвердили это эксериментально. Они полагали, что Wnt служит в качестве коротко-действующего активатора, а Dkk в качестве дально-действующего ингибитора, в этой системе (28). Эта пара факторов 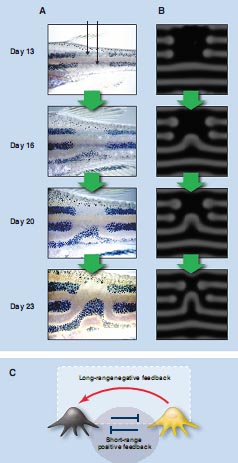 Fig. 3. Movement of zebrafish stripes and the interaction network among the pigment cells. The pigment pattern of zebrafish is composed of black pigment cells (melanophores) and yellow pigment cells (xanthophores). The pattern is made by the mutual interaction between these cells. (A) Melanophores in the two black stripes were ablated by laser, and the process of recovery was recorded. (B) Results of simulation by the Turing model. (C) Interaction network between the pigment cells deduced by experiments. The red arrow represents a long-range positive (enhancing) effect, whereas the blue line with the end bar represents a short-range negative (inhibitory) effect. A circuit of two negative interactions functions as a positive feedback.
Fig. 3. Movement of zebrafish stripes and the interaction network among the pigment cells. The pigment pattern of zebrafish is composed of black pigment cells (melanophores) and yellow pigment cells (xanthophores). The pattern is made by the mutual interaction between these cells. (A) Melanophores in the two black stripes were ablated by laser, and the process of recovery was recorded. (B) Results of simulation by the Turing model. (C) Interaction network between the pigment cells deduced by experiments. The red arrow represents a long-range positive (enhancing) effect, whereas the blue line with the end bar represents a short-range negative (inhibitory) effect. A circuit of two negative interactions functions as a positive feedback.функционирует в различных паттерн-формирующих процессах также, давая такие же критически важные результаты, намекая на широкую роль их для Turing паттернов в развитии (Fig. 4). Интересно, что рост новых волосков базируется на взаимодействиях между соседними фолликулами, что происходит даже у взрослых мышей и в одном случае был идентифицирован мутант, у которого перемещение волны формирования волосков постепенно движется поперек кожи в ходе жизни животных, несущих эту мутацию (29). Plikus et al.(29) показали, как факторы FGF (fibroblast growth factor) и BMP (bone morphogenetic protein) действуют, чтобы генерировать перемещение волны (случай V в модели Turing). Other Potential Turing-Driven Developmental Phenomena Становление лево-правостронней асимметрии у позвоночных запускается однонаправленной ротацией ресничек узелка, сопровождаемой взаимодействием Nodal и Lefty , кеоторое умножает и стабилизирует тонкие отличия в экспрессии генов (30, 31). Nodal усиливает как собственную экспрессию, так и Lefty,тогда как Lefty ингибирует активность Nodal. Тот факт, что Lefty распространяется дальше, чем Nodal указывает на то, что ингибирующее взаимодействие распространяется быстрее, чем его активирующий противник (counterpart), всё это указывает на то, что эта система удовлетворяет фундаментальным потребностям формирования паттерна Turing (30) (Fig. 4).
В развитии конечностей позвоночных конденсации предхряща, которые позднее заместятся костями скелета, возникают периодически вдоль передне-задней оси области дистального конца. Поскольку это формирование паттерна осуществляется без какого-либо периодического препаттерна, то модель Тьюринга, как полагают, описывает лежащий в основе механизм (32). В этой системе, transforming growth factor-β (TGF-β) выступает в качестве кандидата на роль молекулы активатора (33). TGF-β может стимулировать свою собственную продукцию запускать конденсацию предхряща и эти сайты зарождающейся конденсации оказывают латерально действующий ингибирующий эффект на хондрогенез. Хотя нет кандидата на роль ингибитора, сеть взаимодействий, представляющая функцию TGF-β и конденсацию предхряща может удовлетворять критериям коротко-дейстующей активации и дально-действующего ингибирования (33). Miura and Shiota показали, что почти периодические пространственные паттерны хондрогенеза наблюдаются в культуре диссоциированных клеток конечностей in vitro,
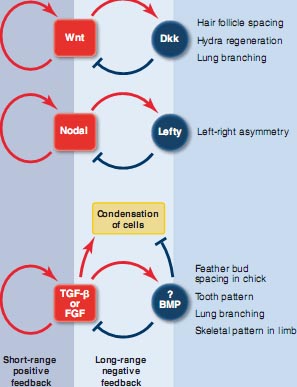 Fig. 4. Possible networks of protein ligands may give rise to Turing patterns in the embryo. Shown above are candidates for the RD mechanism proposed by molecular experiments. For a detailed explanation of each network, refer to the text and the articles listed in the references. In all these cases, the network is identical to that of the activator-inhibitor model proposed by Gierer and Meinhardt (17). Condensation of cells by migration into a local region causes sparse distribution of cells in a neighboring region. This can also function as long-range inhibition. (Note that the involvement of the RD mechanism in some of the phenomena above has not been fully accepted by experimental researchers.)
Fig. 4. Possible networks of protein ligands may give rise to Turing patterns in the embryo. Shown above are candidates for the RD mechanism proposed by molecular experiments. For a detailed explanation of each network, refer to the text and the articles listed in the references. In all these cases, the network is identical to that of the activator-inhibitor model proposed by Gierer and Meinhardt (17). Condensation of cells by migration into a local region causes sparse distribution of cells in a neighboring region. This can also function as long-range inhibition. (Note that the involvement of the RD mechanism in some of the phenomena above has not been fully accepted by experimental researchers.)и что добавление TGF-β меняет паттерн в соответствии с предсказаниями модели Тьюринга (34). Wnt и Dkk также важны для ветвления дёгких у позвоночных (35) и играют ключевую роль в регенерации головы гидры (36), при которой участие Turing механизма было подтверждено теоретическими и экспериментальными исследованиями. Участие некоторых молекул косвенно доказывают, что работает тот же самый динамический механизм. Однако поскольку они составляют само-регулирующуюся систему, которая устойчива к искусственным пертурбациям, разумно ожидать, что Turing механизм может лежать в основе этого феномена, как это происходит в коже. Watanabe et al. показали, что передача сигналов посредством щелевых соединений (connexin41.8) играет ключевую роль в формировании пигментного паттерна у рыбок данио (37). Потеря функции connexin гена (leopard) снижает пространственную периодичность и изменяет паттерн полос на точки (37). Мутация др. гена щелевых соединений, connexin43, укорачивает каждый луч плавника, давая укороченные плавники (38). Хотя детальный молекулярный механизм, лежащий в основе этого феномена ещё не выяснен, возможно, что тот же самый механизм действует и в др. процессах развития животных. Приведенные выше примеры ни в коем случае не исчерпывают список кандидатов, исследуемых как потенциал биологических Turing паттернов. Более детальные обсуждения см. (4) и (6).
Идентификация специфических динамик RD систем является критической для демонстрации пригодности Turing механизма к формированию данного паттерна. В случае формирования пигментного паттерна возможно нарушать паттерн и наблюдать процесс регенерации. В большинстве др. систем такие наблюдения осложняются, поскольку экспериментальные вмешательства могут быть летальными. Это одна из причин, почему трудно продемонстрировать RD активность в некоторых биологических системах. (В SOM Text 1- 4, мы суммируем важные моменты для исследователей, чтобы держать в голове, когда они используют RD модель в качеству рабочей гипотезы.) Недавние технологические успехи в imaging технологиях помогают таким исследованиям. Более того, искусственная генерация Turing паттернов в клеточных культурах позволит в ближайшем будущем создать синтетическую биологию (39).
|